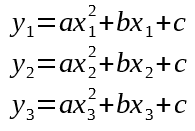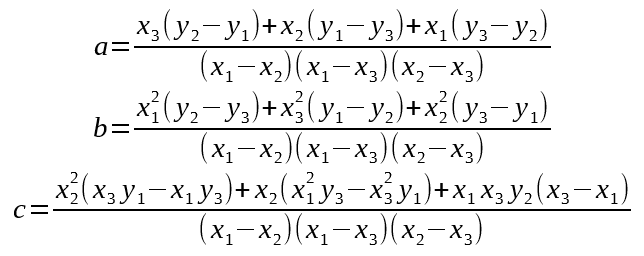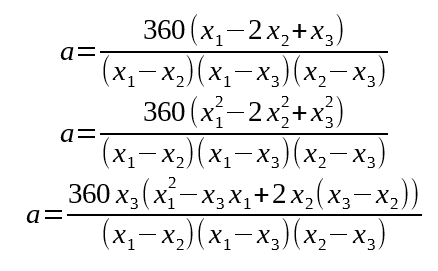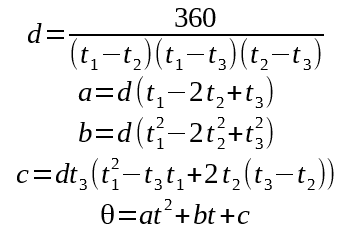In my last post, I introduced two sets of algorithms. One to run a beacon-only system, the other an accelerometer system. The algorithms were fairly easy to work out the math for, and fairly easy to express in code.
But say you need better. Say you need a perfect flicker display, or the easiest-to-control meltybrain bot possible. If you're that kind of builder (I am, at least), then you're in luck. We can take these algorithms a step further. The math is harder (read: longer), so I'm splitting this up into a post for both sensing systems.
Beacon Sensing, part 2
In the previous post, I showed graphs with beautiful, straight lines. The original algorithm works great if this is the case. But what if it's not the case? What if, for instance, the bot is accelerating?
As you can see, the prediction diverges from reality. Our algorithm expects a line, but the robot is accelerating. We get a parabola instead. The error resets at every measurement, so this may not be an enough of an issue for the typical meltybrain. But if you made it past the first paragraph of this post it must be an issue for you.
What if instead of keeping track of the last two edges, we keep track of the last three?
If we assume that all three points are on the same parabola, we can calculate the equation of the parabola and use it to find where we are now. The parabola equation is:
The equation has three constants we need to solve for. Fortunately we have three prior points to help us do that: (x1, y1), (x2, y2), and (x3, y3), where x1 is earlier and x3 is later.
Represented in matrix form:
Solving for a,b,c:
We can simplify by understanding that y1=-720, y2=-360, and y3=0.
Now lets pull the common "d" parameter off and substitute in more appropriate variables:
The Final Equations:
Where t1-t3 are the measurement times (t1 being earliest), t is the current time, and Θ is the calculated angle. a, b, c, d only need to be recalculated at every beacon edge. Θ is calculated on every iteration. Here's what our graph looks like now:
These equations should work even if the bot is not accelerating. There will still be error in your calculation if your acceleration varies over time, but those events tend not to last very long.
An additional gotcha you should know about with either beacon algorithms (linear or parabolic) is that missed beacon edges can severely disturb your predictions. The bot will think it's spinning much slower since the edges it saw were so far apart. This disturbance lasts longer in the parabolic algorithm since the "memory" of the event lasts an additional 360º. Clever code can handle missed triggers, but it will need to be specifically coded in.
Thanks to teammate Novia Berriel for working out the math